大阪大学基礎工学部機械工学同窓会Alumni Association of Department of Mechanical Engineering

【機能デザイン領域 杉山 和靖 教授】

マイクロ流路を流れる柔らかい粒子の集まり方を解明
－スーパーコンピュータ「富岳」が解き明かす，細胞選別の新原理－

・マイクロ流路内における粒子の集束パターンが、粒子の変形性によって劇的に変化することを明らかに

・マイクロ流路内の粒子集束の研究は硬い粒子を中心に行われており、細胞のような柔らかい粒子の挙動は十分に理解されておらず、数値計算による予測はあったが、実験的な検証が不足していた

・細胞サイズのやわらかいヒドロゲル粒子（※1）を作製する技術を確立し、実験的に柔らかい粒子の集束挙動の検証、「富岳」を用いた大規模数値計算と新たな理論モデルによって、集束パターンの変化メカニズムを解明

・体の中の細胞や粒子の変形性を利用した次世代のマイクロ流体デバイス開発やがんの早期診断を実現する生体細胞の選別・分離技術への応用が期待

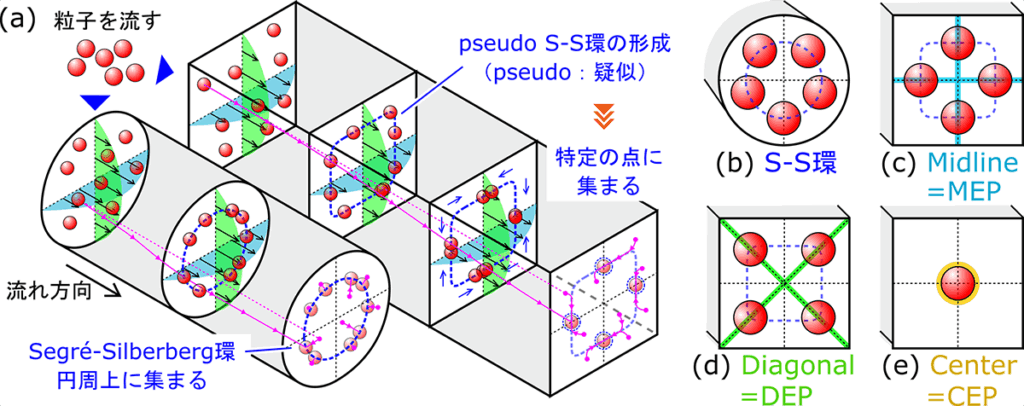
大阪大学大学院基礎工学研究科 廣畑佑真さん（博士後期課程）、杉山和靖教授（理化学研究所光量子工学研究センター 客員研究員兼任）、関西大学システム理工学部 関眞佐子教授、板野智昭教授、佐井一総さん（修士課程（当時））、丹下祐希さん（修士課程（当時））、 西山朋宏さん（修士課程）、岡山大学学術研究院環境生命自然科学学域 鈴木大介教授、湊遥香講師（特任）らの研究グループは、マイクロ流路内における粒子の集束パターンが粒子の慣性と変形性によって劇的に変化することを明らかにしました。硬い粒子が流路の壁近くに集まるのに対し、やわらかいヒドロゲル粒子は流路断面の中心や対角線上に集まることを実証しました。

さらに、スーパーコンピュータ「富岳」（※2）を活用したコンピューターシミュレーション（※3）や、新たな理論モデルに基づく解析により、レイノルズ数（※4）とキャピラリー数（※5）をパラメーターとする相図を作成し、集束パターンが劇的に変化する「相転移（※6）」の条件や、その背景にある物理の仕組みを明らかにしました。この成果は、液体の中の細胞や粒子の変形性を利用した次世代のマイクロ流体デバイス開発につながり、高効率な細胞選別技術として、がんの早期発見など医工学分野への応用が期待されます。

本研究成果は、流体力学に関する専門学術誌である「Journal of Fluid Mechanics」に、2025年9月18日付で公開されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

【用語説明】
（※1）ヒドロゲル粒子
水分子を吸収して内部に閉じ込めたやわらかい材料でできた粒子です。架橋密度や組成を調整することで、やわらかさを調整することができます。変形しやすい性質を活かして、液体中の細胞の動きを調べるためのモデルとして使われることがあります。

（※2）スーパーコンピュータ「富岳」
スーパーコンピュータ「京」の後継機として理化学研究所が設置し、2021年3月から共用を開始した計算機。2025年6月のGraph500ランキングで11期連続1位を獲得。また、TOP500では7位、HPCG(High Performance Conjugate Gradient)では2位、HPL-AI Mixed Precision(HPL-MxP、旧名HPL-AI)では6位を獲得するなど、世界トップレベルの性能を持っています。

（※3）コンピューターシミュレーション
現象の法則を表す数式をコンピューターで計算し、その現象をコンピューター上で再現することです。例えば、天気予報では、空気や水の動きなどのコンピューターシミュレーションによって未来の天候を予測しています。コンピューターシミュレーションは「理論」と「実験」に続く新しい研究方法であり、「第3の科学」と呼ばれます。コンピューターシミュレーションは実験が難しい問題を解決したり、製品開発の試作コストや手間を減らしたり、不思議な現象の仕組みを解き明かしたりするときに本領を発揮します。

（※4）レイノルズ数
流体の慣性力と粘性力との比を表す無次元数です。レイノルズ数は、流れが層流か乱流かを決める指標として使われます。私たちの研究では層流のみを扱っていますが、層流に限った条件でも、レイノルズ数が大きいほど、流れがまっすぐに進もうとする性質が強くなったり、粒子の周りの渦が強くなったりと、流れにレイノルズ数の影響が出てきます。

（※5）キャピラリー数
流体の粘性力と固体の弾性力の比を表す無次元数です。柔軟な粒子の場合、キャピラリー数が大きいほど変形しやすくなります。

（※6）相転移
たとえば水の温度を上げていくと氷から水、水から水蒸気へと融点、沸点を境に状態がガラッと変わることを相転移と呼びます。私たちは、特定のレイノルズ数とキャピラリー数を境に、粒子の集まる位置がガラッと変わることを研究しました。本稿では、この劇的変化を「集束パターンの相転移」と呼んでいます。

Last Update : 2025/10/17

【生体工学領域 大谷 智仁 准教授】

MRIは脳の水の動きを直接測れるか？
－MRIと流体工学の融合による新理論の開発－

・MRIを使って脳内の水の動態を直接推定できる、新しい理論的枠組みを構築

・従来の計測法では脳内の水のような遅い流れの正確な定量化は困難だったが、流体工学の観点からMRI信号理論を再構築することで、MRI信号が本来含んでいる流れの情報の抽出を実現

・脳脊髄液の流れや脳内の老廃物排出システムの解明に役立つことが期待され、将来的には認知症や神経疾患の新しい診断手法の開発につながる可能性に期待

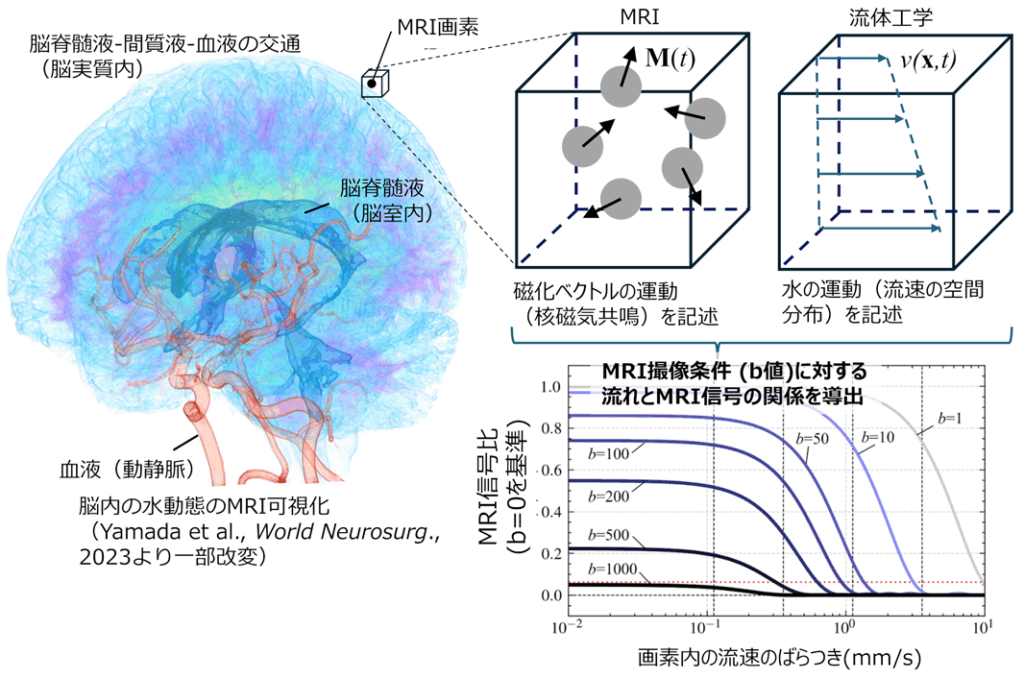
大阪大学大学院基礎工学研究科の大谷智仁准教授、和田成生教授、北海道大学の尾藤良孝特任講師、名古屋市立大学の山田茂樹准教授、滋賀医科大学の渡邉嘉之教授による研究グループは、脳脊髄液（※1）など、頭蓋内や脳内の水の動きをMRIから定量的に推定するための汎用的な理論の構築に成功しました。

従来のMRIによる流れ計測では、脳脊髄液のような遅い流れの定量化は難しく、水分子の拡散を計測する方法である「拡散強調MRI」を応用し、「見かけの拡散係数」により間接的に評価してきました。これまでにも、見かけの拡散係数から流れの情報を抽出する試みが行われてきましたが、多くは特定の条件での仮定にとどまり、一般的に適用できる理論がなく、計測情報の定量性が大きな課題になっていました。

本研究グループは、流れ場の性質を説明する流体工学と核磁気共鳴方程式に基づき、MRI信号の成り立ちを再考しました。そして、見かけの拡散係数が流速分布のばらつきと対応することを示すとともに、MRIの信号が本来持つ流れの情報の解明に成功しました。この成果は、脳内の水の動き、すなわち、脳脊髄液の流れや老廃物除去システムの解明への応用や新たな診断・治療法開発への貢献が期待されます。

本研究成果は、国際磁気共鳴医学会が発行する科学誌「Magnetic Resonance in Medicine」に、９月５日（金）公開されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

【用語説明】
（※1）脳脊髄液
脳の内外に充満する無色透明の液体。

Last Update : 2025/10/16

【非線形力学領域・垂水 竜一 教授】

結晶欠陥の表裏一体関係の起源
－柔らかい幾何学による並進・回転欠陥の新しい見方－

・並進と回転を特徴とする二つの異なる結晶欠陥（※1）の間に指摘されてきた等価性の起源を解明

・これまで、二つの欠陥を包括する理論的枠組みの整備は十分進められておらず、両者に同等のひずみ場が現れる根本的なメカニズムは未解明だった

・柔らかい幾何学「リーマン・カルタン多様体（※2）」に基づく統一理論の整備を進め、この課題を解決

・両者を幾何学的な共通の物差しで整理することが可能となり、近年注目されている回位による材料強化を理解する土台としての応用に期待

大阪大学大学院基礎工学研究科の小林舜典助教、大学院生の武政勝己さん（当時博士前期課程）、垂水竜一教授らの研究グループは、結晶中の「刃状転位」と「くさび回位」が等価なふるまいを示す仕組みを明らかにしました。両者は、規則的な原子配列からなる結晶に含まれた不規則な欠陥構造です。

欠陥の周囲に生じるひずみ場は結晶の強度や靱性を左右するため、材料科学分野での重要な研究対象とされています。これまで、一列に並んだ刃状転位の端部にくさび回位と同等のひずみ場が現れることは知られていましたが、その根本的なメカニズムは不明でした。

今回、研究グループは空間を柔軟にゆがませることのできる幾何学「リーマン・カルタン多様体」に基づく結晶欠陥理論の整備を進め、両者がアフィン接続（※3）と呼ばれる幾何学的構造のみで区別され、それ以外の骨組みが同一となることが、ひずみ場の等価性の起源であることを明らかにしました。さらに、同じ考え方は単独の刃状転位にも適用でき、正負のくさび回位双極子モーメントとして再解釈できることが分かりました。本成果は、優れた特性を持つ新しい結晶材料の設計方針に活用できると期待されます。

本研究成果は、英国科学誌「Royal Society Open Science」に、7月16日（水）8時（日本時間）に公開されました。

詳細は大阪大学ホームページ（ResOU）をご参照ください。

【用語説明】
（※1）結晶欠陥
理想的な結晶は規則的な原子配列からなるが、現実的には原子配列の規則性を破る様々な欠陥が多数内在している。原子配列の並進対称性を破る転位と、回転対称性を破る回位はその代表例である。いずれも対称性の破れた領域が線状に連なった線欠陥に分類される。

（※2）リーマン・カルタン多様体
平坦なユークリッド空間でのベクトルの内角（計量）と平行移動操作（アフィン接続）を一般化した空間の一種で、微分幾何学という数学を土台としている。空間の幾何学的な特徴は捩率と曲率という構造に代表される。結晶欠陥理論への応用は我が国の研究者である近藤一夫や甘利俊一らによって1950年代から進められた。この空間では転位を捩率、回位を曲率として表現することができる。

（※3）アフィン接続
リーマン・カルタン多様体上のベクトルの平行移動を記述する幾何学的構造。通常の平坦なユークリッド空間では、ベクトルを平行移動しても向きも大きさも変わらないが、リーマン・カルタン多様体上ではこれらが変化しうる。アフィン接続がその特性を決定している。

Last Update : 2025/07/31