大阪大学基礎工学部機械工学同窓会Alumni Association of Department of Mechanical Engineering

【非線形力学領域・垂水 竜一 教授】

ゴムの鋭い亀裂は粘弾性から生じる
－ノーベル賞受賞者30年来の理論を証明－

・ゴムが一瞬で壊れる「高速破壊」時に、なぜ亀裂先端が鋭くとがるのかは長年未解明だった。

・ノーベル物理学賞受賞者ド・ジェンヌ博士が提唱した「粘弾性トランペット理論」を連続体力学の基礎方程式から初めて導き、ゴムの基本的性質である粘弾性だけで鋭化が生じることを数学的に証明した。

・タイヤから医療材料まで、幅広いポリマー材料の破壊制御や耐久性向上の理論的基盤となることが期待される。

JST 戦略的創造研究推進事業において、大阪大学 大学院基礎工学研究科の長滝谷 北斗 大学院生（博士後期課程）、小林 舜典 助教、垂水 竜一 教授とZEN大学 知能情報社会学部 作道 直幸 准教授（兼：東京大学 大学院工学系研究科 特任准教授）の研究グループは、ゴムの高速破壊の際に亀裂先端が鋭くとがるメカニズムを、世界で初めて数学的に解明しました。

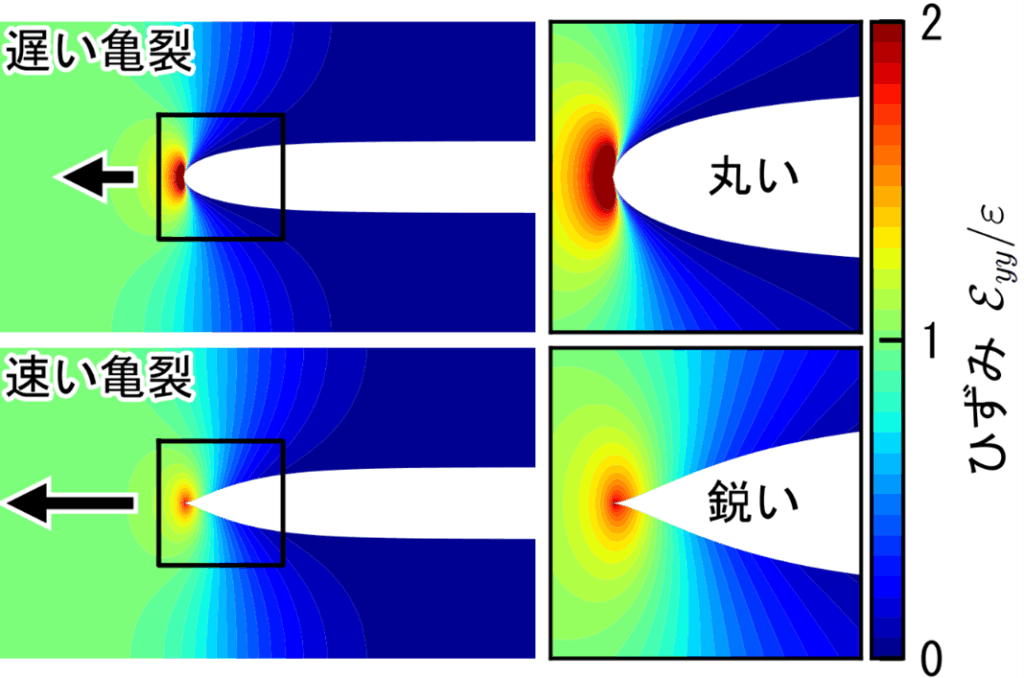
ゴム風船が割れたり、タイヤが破裂（バースト）したりするのは、微小な亀裂が一瞬で広がる「高速破壊」によるものです。このとき、亀裂先端が鋭化し破壊が加速しますが、なぜ鋭化するのかは長年解明されておらず、従来は材料の複雑な非線形効果（※1）が原因と考えられてきました。

本研究グループは、亀裂進展の問題を数学的に厳密に解き、亀裂の形状と材料全体の変形を記述する数式を導出しました。これにより、亀裂先端の鋭化が、ゴムなどのポリマー材料（高分子材料）（※2）が持つ基本的な性質である「粘弾性（※3）」だけで生じることを証明しました。さらに、ノーベル物理学賞受賞者ド・ジェンヌ 博士（※4）が約30年前に提唱した「粘弾性トランペット理論（※5）」を、連続体力学（※6）の基礎方程式から数学的に証明しました。

本成果は、タイヤから医療材料まで幅広い粘弾性材料の破壊制御の理論的基盤となり、製品の耐久性向上や事故防止、長寿命化による環境負荷低減への貢献が期待されます。

本成果は、2025年10月1日（現地時間）に米国の学術誌「Physical Review Research」にLetterとしてオンラインで公開されました。

【用語説明】
（※1）非線形効果
材料に加えた力と生じる変形が比例関係から外れることによる効果。通常、小さな変形の範囲では力を2倍にすると変形も2倍になる。しかし大きな変形では、この比例関係が成り立たなくなる。ゴム・ゲル・プラスチックなど、柔らかくよく伸びるポリマー材料では特に顕著に現れる。

（※2）ポリマー材料（高分子材料）
小さい分子（モノマー）が多数つながり、ひも状や網状に結合した分子を高分子（ポリマー）という。高分子からなる材料がポリマー材料である。分子鎖の種類や結合様式により、プラスチック・ゴム・ゲル・繊維など多様な性質を示す。ゴムは長い分子鎖が化学的に架橋した網目構造を持ち、大きく伸びても元に戻る性質がある。ゲルは同様の網目構造に水などの液体を含んだもの。金属より軽量で成形しやすい利点があるが、薄くすると破れやすく、硬くするともろくなるのが課題であり、強靱なポリマー材料の開発が求められている。

（※3）粘弾性
材料が示す弾性（バネ的な性質）と粘性（蜂蜜のようなネバネバした性質）を併せ持つ性質。ポリマー材料では、変形速度により応答が変化する。ゆっくり変形させると柔らかく振る舞い（ゴム状態）、速く変形させると硬くなる（ガラス状態）。中間の速度では粘性によるエネルギー散逸が起こる。この性質により、同じ材料でも亀裂の進展速度によって破壊の様相が劇的に変化する。力に比例して変形が生じる場合を線形弾性、力に比例して流れが生じる場合を線形粘性といい、両者を併せ持てば線形粘弾性という。今回は、線形粘弾性のみで亀裂先端の鋭化が生じることを示した。

（※4）ド・ジェンヌ博士
フランスの理論物理学者（1932-2007）。1991年ノーベル物理学賞受賞。磁性体や超伝導体の研究で開発した理論手法を、高分子や液晶などのソフトマターに応用し、物理学の新分野を開拓した。スケーリング理論と呼ばれる手法で複雑な現象の本質を抽出し、「現代のニュートン」と称される。

（※5）粘弾性トランペット理論
ド・ジェンヌ 博士が1996年に提唱した、粘弾性材料の動的破壊を記述する理論。亀裂周辺を3つの領域に分け、各領域での変形がべき乗則（※8）に従うと予言。亀裂形状がトランペットのように広がることから命名。スケーリング理論とエネルギーバランスから導かれたが、連続体力学との関係は不明だった。本研究により初めて連続体力学の基礎方程式から導出され、30年越しに理論的正当性が証明された。

（※6）連続体力学
物質を原子・分子の集合ではなく連続的な物体として扱い、その変形や流動を偏微分方程式で記述する理論体系。自動車・航空機や橋の安全設計から人工関節などの医療分野まで幅広く応用される。しかし粘弾性材料の動的破壊は方程式が複雑で解析が困難だった。本研究は新しい数学的手法（※7）により、この難問に初めて厳密解を与えた。

（※7）新しい数学的手法
中学校の数学の図形では、適切な補助線を引くことで複雑な問題が簡単に解けることを習う。本研究でも似た発想の転換が鍵となった。ゴムの破壊では、材料全体が時々刻々と変形する複雑な動的問題を扱う。この変形は各点での「変位場」（電場や磁場のように空間の各点で定義されるベクトル量）で表される。本研究では、時間変化する複雑な変位場を、時間変化しない静的な変位場に変換する「補助場」を発見した。この補助場を用いて動的な亀裂進展を静止した亀裂の問題に変換し、比較的簡単な静止した亀裂の問題を解いてから元の動的な亀裂進展の問題に戻すという数学的工夫により、複雑な粘弾性材料の動的破壊に厳密解を与えた。

（※8）べき乗則
物理量の間に「xのn乗に比例する」という関係が成り立つ法則。身近な例として、音の大きさは、音源から2倍離れると1/4に、3倍離れると1/9になる。これは、音源からの距離xの2乗に反比例する（x-2に比例する）というべき乗則が成り立つためである。本研究では、亀裂先端からの距離xに対して、亀裂の開き幅が特定のべき乗（x1/2、x3/2）に従うことを発見した。x1/2は丸い放物線形状、x3/2はとがった形状を表し、べき乗則の指数nを特定することで亀裂形状の全体像を定量的に理解できる。

Last Update : 2025/10/23